data#

This module provides a set of functions for data manipulation. For instance, there are functions to:

Load data from a file.
Save data to a file.
Perform basic operations such as subtraction and factor multiplication.
Cropping the signal within a x-axis interval.
Normalizing and DC-removal.
Phase correcting the signals using cross-correlation.
Phase correcting based on moving window.

Example usage:

>>> import hwpwn.data as d
>>> d.load('sample.csv')
>>> d.signals(['a1', 'a2', 'b1', 'b2'])
>>> d.triggers(['a_T', 'b_T'])
>>> d.hp(cutoff=10e3, order=3)
>>> d.save(filepath="output.csv.gz")

Between the commands the data is stored in common module, in a variable with name data_aux. The data structure (a dictionary) is shared between the commands and has the following attributes:

x_axis is the x-axis column, a list of numbers.
signals a list of signals.
triggers a list of triggers.
ts the sample period.

For more information refer to the common module documentation.

hwpwn.data.mwxcorr(winsize: str = '3.0e-6', mode: str = 'individual', function: str = 'xcorr', period: int = 6, sigma: float = 0.25, weight: float = 10)#

This command utilizes a parametrizable cross-correlation technique with a moving window to correct for signal lag. Rather than applying the correction to the entire signal at once, it is applied within a moving window, as illustrated in the following image.

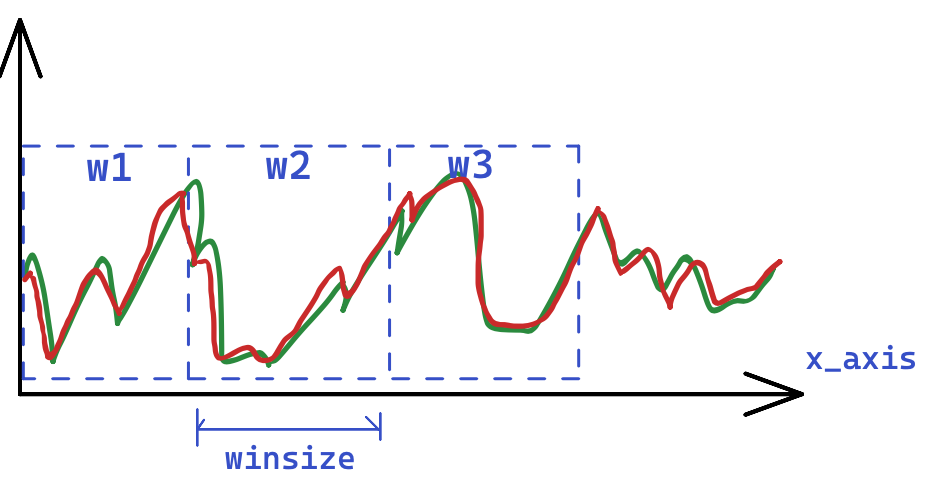
For each window, a function can be selected to calculate the best corrective lag. This is given by the function argument.

The diff, will calculate the sum of absolute error (SAE) and return the lag with the minimum SAE.
The diffp is a period-penalizing version of diff, where periodic lags become less likely.
The xcorr will use the well known cross-correlation function.

Now, having multiple lag values, one for each window, this command can use these lags differently, depending on the mode argument.

The individual mode, each window lag is used individually.
The average mode, the average lag is employed in all windows.
The consensus mode, where the most frequent lag is employed in all windows.

Parameters:

winsize¶ (str) – The window size in x-axis units.
mode¶ (str) – The operation done in the lags of each window. This argument can accept multiple values. Possible values are: “individual”, “average”, “consensus”.
function¶ (str) – The function to calculate the lag in each window. This argument can accept multiple values. Possible values are: “diff”, “diffp”, “xcorr”.
period¶ – Is only used with diffp function and is the lag period in vector index units. Lags of this value will be avoided with diffp function.
sigma¶ – Is only used with diffp function and corresponds to the square root of the variance of the Guass curve.
weight¶ – Is only used with weight function and is a scaling factor for the penalizing term. The higher this value, the more effect the penalizing term has in the lag calculation.

hwpwn.data.triggers(names: list[str])#

From the list of triggers, include only the ones specified by the names argument. For example, if there is trigger x1_T, x2_T, x3_T and one uses the triggers command with names set to ["x2_T"], the output data will only contain x2_T trigger as well as the data signals.

Parameters:: names¶ – the trigger names to include in the output data.

hwpwn.data.min_max(max_win: int = 5, min_win: int = 5)#

This function tries to identify the minimum and maximum points of the signals.

Warning

This function is experimental. It returns a different data structure compared to the other functions. In addition of signal vector, the returning signal will have also markers and markers_x. The reason is that the x-axis will be different, it will not be temporal based, but index based.

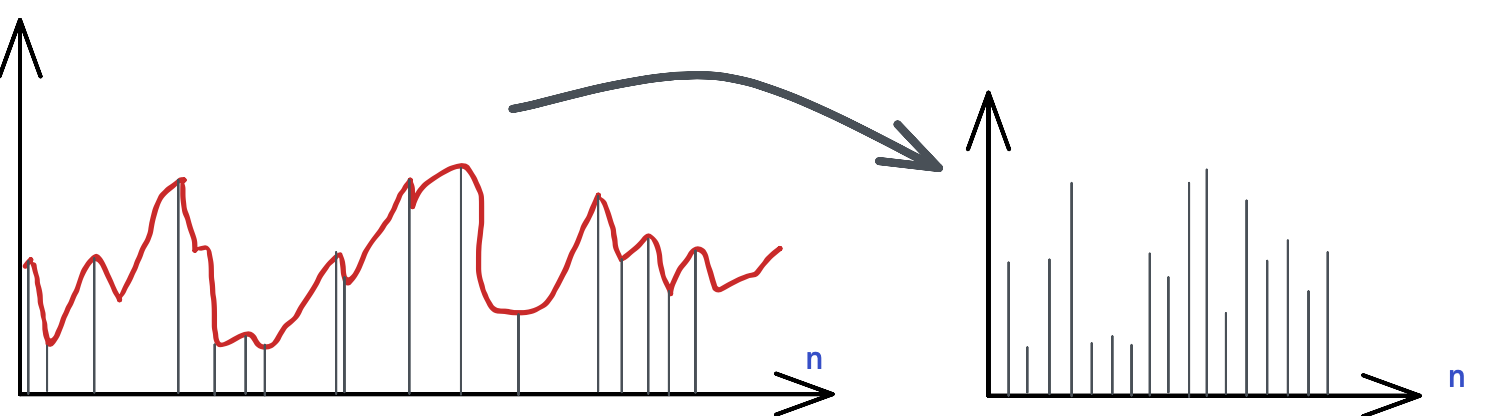
As shown in the plots above, the minimum and maximum values are calculated and returned as a list.

Note

It’s assumed that the signals are oscilating and the lookup will alternate between minimum and maximum values. Thus, this function doesn’t support looking for groups of minimum points or maximum points in sequence.

Parameters:

max_win¶ – Number of points to wait for holding the last maximum value. If the maximum value doesn’t change within this number of points, the maximum is added to the list. By default this is 5.
min_win¶ – Number of points to wait for holding the last minimum value. If the minimum value doesn’t change within this number of points, the minimum is added to the list. By default this is 5.

hwpwn.data.markers2signals()#: Converts markers to signals so that they can be plotted directly using plot functions.

hwpwn.data.xcorr(capidx: int | None = None, refname: str | None = None)#

Corrects signal lag by employing cross-correlation.

Parameters:

capidx¶ – The maximum lag index value.
refname¶ – The reference signal name to use as comparison.

hwpwn.data.process_raw_table_signals(header: list[str], raw_data: list[list])#

Internal function to process table data from header list and raw data information. The header list is just a list of strings that correspond to the column names. The raw_data is a list of rows. Each row is a list of values which are converted to float.

Example usage:

>>> cols = ['t', 'a', 'b']
>>> rows = [[1, 10, 11], [2, 11, 13], [3, 9, 15]]
>>> s, t = process_raw_table_signals(header=cols, raw_data=rows)

Parameters:

header¶ (list[str]) – List of strings corresponding to the column names.
raw_data¶ (list[list]) – List of rows, where each row is another list of strings or numbers. The items in the row will be converted to float.

hwpwn.data.load_csv(filepath: str, xscale: float = 1e-06)#

Loads a CSV file into a data structure that is easier to use for signal processing and plotting. This function expects a CSV with the time in the first column and signal voltages in the following columns. The first line must have the signal labels. If the label starts with character T, it’s considered to be a trigger signal. There can be more than one trigger signal in the file.

Note

The load command can accept multiple file types and call the correct load function. No need to call this command for CSV files if the file has a .csv extension.

Parameters:

filepath¶ – The file to load.
xscale¶ – The x-axis scale to seconds. Each x-axis value will be multipled by xscale from and divided by scale parameter of configuration as follows:

\[x_i' = x_i * \mathrm{xscale}/\mathrm{cfg\_scale}\]

So for example, if cfg_scale is 1e-6 (meaning that we want to use common unit of x-axis in microseconds), and xscale is 1e-9 (meaning that the x-axis values units are in nanoseconds), and the CSV has the x-axis (230.0, 250.0, 410.0) the data stored in memory will have the x-axis values (0.230, 0.250, 0.410).

hwpwn.data.load_csvz(filepath: str, xscale: float = 1e-06)#

This command is very similar to the load_csv() command, except that the CSV file is compressed using gzip. The first column is loaded as the x-axis, and signal voltages (including the triggers) are loaded from the following columns.

To distinguish between trigger signals and normal signals, a suffix should be used. If a column name ends with the characters _T or _HT, it is considered to be a trigger signal. There may be more than one trigger signal in the file.

Note

The load command can accept multiple file types and call the correct load function. No need to call this command for CSVZ files if the file has a .csvz extension.

Parameters:

filepath¶ – The file to load.
xscale¶ – The x-axis scale to seconds. Each x-axis value will be multipled by xscale from and divided by scale parameter of configuration as follows:

\[x_i' = x_i * \mathrm{xscale}/\mathrm{cfg\_scale}\]

hwpwn.data.load(filepath: str, format: str = 'auto', xscale: float = 1e-06, append: bool = False)#

Loads data from a local file. The file format can be: compressed CSV (.csv.gz) or CSV (.csv). The format is automatically determined from the filename extension. To override the format argument can be provided.

Each x-axis value will be multipled by xscale from and divided by scale parameter of configuration as follows:

\[x_i' = x_i * \mathrm{xscale}/\mathrm{cfg\_scale}\]

hwpwn.data.save(filepath: str, format: str = 'csv.gz')#

Saves the current data to a file. By default the format is compressed CSV file (.csv.gz).

Parameters:

filepath¶ – Where to save the current data in memory.
format¶ – The format of the file. Supported values are: csv, or csv.gz.

hwpwn.data.signals(names: list[str])#

Filters the input signals to retain only the signals whose names are specified in the names argument.

Parameters:: names¶ (list[str]) – List of signal names to retain.

hwpwn.data.xzoom(xstart: float | None = None, xend: float | None = None)#

Filter data from a specific x-axis interval, so triggers, time axis and signal will be copied and only points between xstart and xend will remain. If xstart is None or xend is None, it will default to the minimum or maximum value accordingly.

Parameters:

xstart¶ (float) – Start x-axis value of the interval to retain. If None defaults to minimum x-axis value.
xend¶ (float) – End x-axis value of the interval to retain. If None defaults to maximum x-axis value.

Example usage:

>>> xzoom(xstart=10, xend=20)

If the configuration scale is set to 1e-6, this means it will crop the signals between 10us and 20us.

hwpwn.data.subtract(pos: str, neg: str, dest: str, abs: bool = False, append: bool = False)#

Subtract two signals and save the result in a new signal name. It supports appending to existing signals and also the absolute value calculation (turning this into an Absolute Error calculation command).

Parameters:

pos¶ – The positive term of the difference, a signal name.
neg¶ – The negative term of the difference, a signal name.
dest¶ – The signal name to store the result of the subtraction.
append¶ – If set True, the original signals are retained.
abs¶ – If set True, calculates the absolute of the subtraction before saving the value.

hwpwn.data.multiply(source: str, multiplier: float, dest: str, append: bool = False)#

Multiply two signals with multiplier and save the result in a new signal. If append is not set, the previous data structure is cleared and only the new signal will persist.

Parameters:

source¶ – Source signal to multiply with the multiplier value.
multiplier¶ – Value to multiply source signal values with.
dest¶ – Destination signal name.
append¶ – If set True, the original signals are retained.

hwpwn.data.average(name: str = 'avg_signal', append: bool = False)#

Generates a new signal that is the average of the existing signals. More specifically, this function does:

\[\bar{x}[n] = \frac{1}{M} \sum_{i=1}^{M} x_i[n]\]

The resulting signal, \(\bar{x}[n]\), is the average of the other signals given by \(x_i[n]\).

Parameters:

name¶ – The output signal name. By default, the new signal name is ‘avg_signal’.
append¶ – If set True, the original signals are retained.

hwpwn.data.remove_mean()#

Remove the signal mean. For each signal, the mean is calculated and then, each point of the signal is subtracted by this mean value.

\[x_{new}[n] = x[n] - \frac{1}{N} \sum_{n=0}^{N-1} x[n]\]

The new signal \(x_{new}[n]\) is the orignal signal \(x[n]\) subtracting the mean value.

hwpwn.data.normalize()#

Normalize the signals based on minimum and maximum values.

\[x_{norm}[n] = \frac{x[n] - \min_{n}(x[n])}{ \max_{n} (x[n]) - \min_{n} (x[n])}\]

The normalization will make the resulting signal have a maximum value of 1.0 and a minimum value of 0.

hwpwn.data.hp(cutoff: float, order: int = 5, append: bool = False, append_prefix: str = 'fhp')#

Apply linear high-pass filter based on Butterworth polynomial to all the signals (except triggers).

Parameters:

cutoff¶ – The cutoff frequency (in Hertz) of the high-pass filter.
order¶ – The order of the Butterworth polynomial, which has direct impact in the steepness of the transition between the passband and the stopband. By default, an order of 5 is used.
append¶ – If set True, the original signals are retained.
append_prefix¶ – If append is True, this is the prefix used for the new signal names.

hwpwn.data.denoise(wavelet: str = 'db8')#

Apply Wavelet-based denoising of the signals.

Parameters:: wavelet¶ – The name of the wavelet to use for the denoising.

Warning

This function is experimental.